Regra de Simpson

Na análise numérica, a regra ou método de Simpson (chamada así na honra de Thomas Simpson) é un método de integración numérica que se utiliza para obter a aproximación da integral:

A función f(x) (azul) é aproximada por unha función cuadrática P(x) (vermello).

$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right]$.

Derivación da regra de Simpson

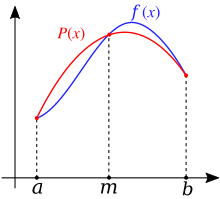
Consideramos o polinomio interpolante de orde dous $\mathrm {P_{2}(x)}$, que se aproxima a función integrando $\mathrm {f(x)}$ entre os nodos x₀ = a, x₁ = b e m = (a+b)/2. A expresión dese polinomio interpolante, expresado a través da Interpolación polinómica de Lagrange é:

$P_{2}(x)=f(a){\frac {(x-m)(x-b)}{(a-m)(a-b)}}+f(m){\frac {(x-a)(x-b)}{(m-a)(m-b)}}+f(b){\frac {(x-a)(x-m)}{(b-a)(b-m)}}.$

Así, a integral buscada pódese aproximar como:

$\int _{a}^{b}f(x)\,dx\approx \int _{a}^{b}P_{2}(x)\,dx={\frac {h}{3}}\left[f(a)+4f(m)+f(b)\right].$

Erro

O erro de aproximar a integral mediante o método de Simpson é

$-{\frac {h^{5}}{90}}f^{(4)}(\xi ),$

onde $h=(b-a)/2$ e $\xi \in [a,b]$.

Regra de Simpson composta

No caso de que o intervalo [a,b] non sexa o suficientemente pequeno, o erro ao calcular a integral pode ser moi grande. Para iso, recórrese á fórmula composta de Simpson. Dividiremos o intervalo [a,b] en n subintervalos iguais, de xeito que $x_{i}=a+ih$, onde $h=(b-a)/n$ para $i=0,1,...,n$.

Aplicando a Regra de Simpson a cada subintervalo, temos:

$\int _{x_{j-1}}^{x_{j}}f(x)\,dx={\frac {x_{j}-x_{j-1}}{6}}\left[f(x_{j-1})+4f\left({\frac {x_{j-1}+x_{j}}{2}}\right)+f(x_{j})\right]j=1,...,n.$

Sumando as integrais de todos os subintervalos, chegamos a que:

$\int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+2\sum _{j=1}^{n/2-1}f(x_{2j})+4\sum _{j=1}^{n/2}f(x_{2j-1})+f(x_{n}){\bigg ]},$

O máximo erro vén dado pola expresión $-{\frac {h^{4}}{180}}(b-a)f^{(4)}(\xi ).$