Barra de Sheffer
Nas funcións booleanas e no cálculo proposicional, a barra de Sheffer, NAND ("non e") ou non conxunción [1], denota unha operación lóxica que é equivalente á negación da operación de conxunción, expresada en linguaxe común como "non ambas as dúas ao mesmo tempo". En electrónica dixital, corresponde á porta NAND. Leva o nome de Henry Maurice Sheffer e escríbese como ou como ou como ou como en notación polaca por Łukasiewicz (pero non como ||, usado a miúdo para representar a disxunción).
 | |
| Outros nomes | Non E, Not AND |
|---|---|
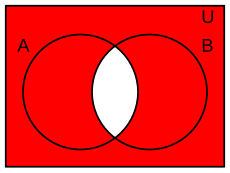
| operador booleano | |
| linguaxe natural | Non (A e B) |
| operador de conxuntos | |
| táboa de verdade | |
| outros símbolos | , , |
| porta lóxica |  |
O seu dual é o operador NOR.
Definición
editarA non conxunción é unha operación lóxica sobre dous valores lóxicos. Produce un valor de verdadeiro, se e só se, polo menos unha das proposicións é falsa.
Táboa de verdade
editarA táboa de verdade é a seguinte.
| F | F | V |
| F | V | V |
| V | F | V |
| V | V | F |
Equivalencias lóxicas
editarA barra de Sheffer de e é a negación da súa conxunción
Segundo as leis de De Morgan, isto tamén é equivalente á disxunción das negacións de e
Notacións e nomes alternativos
editarEn 1913, Sheffer describiu o uso da non disxunción e mostrou a súa integridade funcional. Moitas persoas, comezando por Nicod en 1917, e seguidas por Whitehead, Russell e moitos outros, pensaron erróneamente que Sheffer describiu a non conxunción usando , chamándoo barra de Sheffer.
En 1929, Łukasiewicz utilizou en para non conxunción na súa notación polaca.[2]
Unha notación alternativa para a non conxunción é . Non está claro quen introduciu por primeira vez esta notación, aínda que a correspondente para a non disxunción foi usada por Quine en 1940.[3]
Propiedades
editarNAND é conmutativa pero non asociativa, o que significa que mais .[4]
Completude funcional
editarA barra de Sheffer, tomada por si soa, é un conxunto funcionalmente completo de conectivas.[5][6]
Pódes probar mostrando primeiro, cunha táboa de verdade, que é equivalente como función de verdade a .[7] Logo, xa que é equivalente funcionalmente a , [7] e é equivalente a , [7] a barra de Sheffer abonda para definir o conxunto de conectivas , [7] que se mostra como verdadeiramente completa polo Teorema da forma normal disxuntiva.[7]
Outras operacións booleanas en termos da barra de Sheffer
editarExpresado en termos de NAND , os operadores habituais da lóxica proposicional son:
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
Notas
editar- ↑ Howson, Colin (1997). Logic with trees: an introduction to symbolic logic. Londres; Nova York: Routledge. pp. 43. ISBN 978-0-415-13342-5.
- ↑ Łukasiewicz, J. (1929). Elementy logiki matematycznej (2 ed.). Warszawa: Państwowe Wydawnictwo Naukowe.
- ↑ Quine, W. V (1940). Mathematical Logic (Revised ed.). Cambridge, Londres, Nova York, New Rochelle, Melbourne e Sydney: Harvard University Press. p. 45.
- ↑ Rao, G. Shanker (2006). Mathematical Foundations of Computer Science. I. K. International Pvt Ltd. p. 21. ISBN 978-81-88237-49-4.
- ↑ Weisstein, Eric W. "Propositional Calculus". mathworld.wolfram.com (en inglés). Consultado o 2024-03-22.
- ↑ Franks, Curtis (2023). Zalta, Edward N.; Nodelman, Uri, eds. Propositional Logic. The Stanford Encyclopedia of Philosophy (Fall 2023 ed.) (Metaphysics Research Lab, Stanford University). Consultado o 2024-03-22.
- ↑ 7,0 7,1 7,2 7,3 7,4 Howson, Colin (1997). Logic with trees: an introduction to symbolic logic. Londres; Nova York: Routledge. pp. 41–43. ISBN 978-0-415-13342-5.
Véxase tamén
editar| Wikimedia Commons ten máis contidos multimedia na categoría: Barra de Sheffer |
Bibliografía
editar- Bocheński, Józef Maria; Menne, Albert Heinrich (1960). Precis of Mathematical Logic. Traducido por Bird, Otto (revised ed.). Dordrecht, South Holland, Netherlands: D. Reidel. (NB. Editado e traducido do francés: Précis de logique mathématique)
- Peirce, Charles Sanders (1931–1935). "A Boolian Algebra with One Constant". En Hartshorne, Charles; Weiss, Paul. Collected Papers of Charles Sanders Peirce 4. Cambridge: Harvard University Press. pp. 12–20.






