Cuaternión
| ↓ × → | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
| A columna da esquerda mostra o factor esquerdo, a fila superior mostra o factor dereito. A maiores, e tamén para , . | ||||
En matemáticas, o sistema numérico de cuaternións estende os números complexos. Os cuaternións foron descritos por primeira vez polo matemático irlandés William Rowan Hamilton en 1843[1][2] e aplicados á mecánica no espazo tridimensional. A álxebra dos cuaternións adoita denotarse por H (por Hamilton), ou por Os cuaternións non son un corpo, porque a multiplicación de cuaternións non é, en xeral, conmutativa. Os cuaternións proporcionan unha definición do cociente de dous vectores nun espazo tridimensional.[3][4] Os cuaternións son xeralmente representados na forma
onde os coeficientes a, b, c, d son números reais e 1, i, j, k son os vectores ou elementos da base.
Os cuaternións utilízanse en matemáticas puras, pero tamén teñen usos prácticos en matemáticas aplicadas, particularmente para cálculos que implican rotacións tridimensionais, como en gráficos tridimensionais por ordenador, visión por ordenador, robótica, resonancia magnética[5] e análise de texturas cristalográficas.[6] Pódense empregar xunto a outros métodos de rotación, como os ángulos de Euler e as matrices de rotación, ou como alternativa a eles, segundo a aplicación.
En termos modernos, os cuaternións forman unha álxebra de división normada asociativa de catro dimensións sobre os números reais e, polo tanto, un anel, tamén un anel de división e un dominio. É un caso especial dunha álxebra de Clifford, clasificada como Foi a primeira álxebra de división non conmutativa que se descubriu.
Os cuaternións unitarios dan unha estrutura de grupo nas esferas de S3 isomorfas aos grupos Spin(3) e SU(2), é dicir, o grupo de recubrimento universal SO(3). Os vectores da base positivos e negativos forman o grupo de cuaternións de oito elementos.

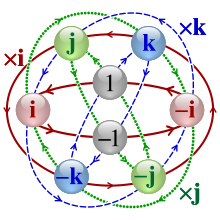
- en azul:
- 1 ⋅ i = i (plano 1/i)
- i ⋅ j = k (plano i/k)
- en vermello:
- 1 ⋅ j = j (plano 1/j)
- j ⋅ i = −k (plano j/k)
Definición
editarUn cuaternión é unha expresión da forma
onde a, b, c, d, son números reais e i, j, k, son símbolos que se poden interpretar como vectores unitarios que apuntan ao longo dos tres eixes espaciais.
Hamilton describe un cuaternión , de forma que consta dunha parte escalar e unha parte vectorial. O cuaternión chámase parte vectorial (ás veces parte imaxinaria) de q, e a é a parte escalar (ás veces parte real) de q.
O conxunto de cuaternións é un espazo vectorial de 4 dimensións sobre os números reais, con como base, pola adición de compoñentes
e a multiplicación escalar por compoñentes
Unha estrutura de grupo multiplicativa, chamada produto de Hamilton, denotada por xustaposición, pódese definir nos cuaternións do seguinte xeito:
- O cuaternión real 1 é o elemento de identidade.
- Os cuaternións reais conmutan con todos os outros cuaternións, é dicir, aq = qa para cada cuaternión q e cada cuaternión real a. En terminoloxía alxébrica isto quere dicir que o corpo dos cuaternións reais é o centro desta álxebra cuaterniónica.
- Primeiro dáse o produto para os elementos básicos (ver subsección seguinte), e despois esténdese a todos os cuaternións utilizando a propiedade distributiva e a propiedade central dos cuaternións reais. O produto de Hamilton non é conmutativo, pero é asociativo, polo que os cuaternións forman unha álxebra asociativa sobre os números reais.
- A maiores, cada cuaternión distinto de cero ten unha inversa con respecto ao produto de Hamilton:
Así, os cuaternións forman unha álxebra de división.
Multiplicación dos elementos da base
editar| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
A multiplicación por 1 dos elementos da base i, j e k defínese polo feito de que 1 é unha identidade multiplicativa, é dicir,
Os produtos dos outros elementos da base son
Combinando estas regras,
Centro
editarO centro dun anel non conmutativo é o subanel dos elementos c tal que cx = xc para todo x. O centro da álxebra de cuaternións é o suborpo dos cuaternións reais. De feito, forma parte da definición que os cuaternións reais pertencen ao centro. Pola contra, se q = a + b i + c j + d k pertence ao centro, entón
e c = d = 0. Un cálculo similar con j en lugar de i mostra que tamén se ten b = 0. Por tanto q = a é un cuaternión real.
Produto de Hamilton
editarPara dous elementos a1 + b1i + c1j + d1k e a2 + b2i + c2j + d2k, o seu produto, chamado produto de Hamilton (a1 + b1i + c1j + d1k) ( a2 + b2i + c2j + d2k ), está determinado polos produtos dos elementos da base e a lei distributiva. A lei distributiva permite ampliar o produto para que sexa unha suma de produtos de elementos da base. Isto dá a seguinte expresión:
Agora os elementos da base pódense multiplicar usando as regras indicadas anteriormente para obter: [7]
Partes escalares e vectoriais
editarUn cuaternión da forma a + 0 i + 0 j + 0 k, onde a é un número real, chámase escalar, e un cuaternión da forma 0 + b i + c j + d k, onde b, c e d son números reais, e polo menos un de b, c ou d é distinto de cero, chámase cuaternión vectorial. Se a + b i + c j + d k é calquera cuaternión, entón a chámase a súa parte escalar e b i + c j + d k a súa parte vectorial. Aínda que cada cuaternión pode ser visto como un vector nun espazo vectorial de catro dimensións, é común referirse á parte vectorial como vectores nun espazo tridimensional. Con esta convención, un vector é o mesmo que un elemento do espazo vectorial [a]
Se un cuaternión se divide nunha parte escalar e unha parte vectorial, é dicir,
entón as fórmulas para a suma, a multiplicación e a inversa multiplicativa son
onde " " e " " indican respectivamente o produto escalar e o produto vectorial.
A conxugación, a norma e a recíproca
editarA conxugación de cuaternións é análoga á conxugación de números complexos e á transposición (tamén coñecida como reversión) de elementos das álxebras de Clifford. Para definilo, temos o cuaternión . O conxugado de q é o cuaternión . Denotase por q∗, qt, ou q.[7] A conxugación é unha involución, o que significa que é a súa propia inversa, polo que conxugar un elemento dúas veces devolve o elemento orixinal. O conxugado dun produto de dous cuaternións é o produto dos conxugados na orde inversa. É dicir, se p e q son cuaternións, entón (pq)∗ = q∗p∗, non p∗q∗.
A conxugación dun cuaternión, en marcado contraste cos complexos, pódese expresar coa multiplicación e adición de cuaternións:
A conxugación pódese usar para extraer as partes escalares e vectoriais dun cuaternión. A parte escalar de p é 1/2(p + p∗), e a parte vectorial de p é 1/2(p − p∗).
A raíz cadrada do produto dun cuaternión co seu conxugado chámase norma e denótase . En fórmulas, isto exprésase do seguinte xeito:
- .
Isto é sempre un número real non negativo, e é o mesmo que a norma euclidiana en considerado como o espazo vectorial . Multiplicando un cuaternión por un número real escala a súa norma polo valor absoluto do número. É dicir, se α é real, entón
Este é un caso especial do feito de que a norma é multiplicativa, é dicir
para dous cuaternións p e q calquera. A multiplicatividade é unha consecuencia da fórmula do conxugado dun produto. Alternativamente, dedúcese da identidade
(onde i denota a unidade imaxinaria habitual) e, polo tanto, a partir da propiedade multiplicativa dos determinantes das matrices cadradas.
Esta norma permite definir a distancia d(p, q) entre p e q como a norma da súa diferenza:
Isto fai de un espazo métrico. A suma e a multiplicación son continuas en relación coa topoloxía métrica asociada. Isto dedúcese exactamente coa mesma proba que para os números reais do feito de que é unha álxebra normada.
Cuaternión unitario
editarUn cuaternión unitario é un cuaternión de norma 1. Dividindo un cuaternión q distinto de cero pola súa norma produce un cuaternión unitario Uq chamado versor de q:
Todo cuaternión distinto de cero ten unha descomposición polar única mentres que o cuaternión cero pode formarse a partir de calquera cuaternión unitario.
Usando a conxugación e a norma permite definir o recíproco dun cuaternión distinto de cero. O produto dun cuaternión co seu recíproco debe ser igual a 1, e as consideracións anteriores implican que o produto de e é 1 (para calquera orde de multiplicación). Polo tanto, o recíproco de q defínese como
Dado que a multiplicación é non conmutativa, as cantidades cocientes p q−1 e q−1p son diferentes (agás se p e q son múltiplos escalares entre si ou se un deles é escalar): a notación
Os cuaternións e a xeometría tridimensional
editarA parte vectorial dun cuaternión pódese interpretar como un vector de coordenadas en polo tanto, as operacións alxébricas dos cuaternións reflicten a xeometría de Operacións como o produto escalar e o produto vectorial poden definirse en termos de cuaternións, e isto fai posíbel aplicar técnicas de cuaternións alí onde xurdan vectores espaciais. Unha aplicación útil dos cuaternións foi interpolar as orientacións de fotogramas clave en gráficos por ordenador.
Para o resto desta sección, i, j e k denotarán os tres vectores da base imaxinarios [9] de e unha base para Substituíndo i por −i, j por −j e k por −k envía un vector ao seu inverso aditivo, polo que o inverso aditivo dun vector é o mesmo que o seu conxugado como un cuaternión. Por esta razón, a conxugación ás veces chámase inverso espacial.
Para dous cuaternións vectoriais p = b1i + c1j + d1k e q = b2i + c2j + d2k o seu produto escalar, por analoxía cos vectores en é
Tamén se pode expresar de forma sen compoñentes como
Isto é igual ás partes escalares dos produtos pq∗, qp∗, p∗q, e q∗p. Teña en conta que as súas partes vectoriais son diferentes.
O produto vectorial de p e q en relación coa orientación determinada pola base ordenada i, j e k é
(Lembre que a orientación é necesaria para determinar o signo.) Isto é igual á parte vectorial do produto pq (como cuaternións), así como á parte vectorial de −q∗p∗ . Tamén ten a fórmula
Para o conmutador, [p, q] = pq − qp, de dous cuaternións vectoriais temos
En xeral, sexan p e q cuaternións e escribimos
onde ps e qs son as partes escalares, e pv e qv son as partes vectoriais de p e q. Logo temos a fórmula
Os cuaternións unitarios pódense identificar con rotacións en e foron chamados versores por Hamilton.[10] Consulte tamén Cuaternións e rotación espacial para obter máis información sobre como modelar rotacións tridimensionais mediante cuaternións.
Representacións en matrices
editarDo mesmo xeito que os números complexos poden ser representados como matrices, tamén poden representarse os cuaternións. Hai polo menos dúas formas de representar os cuaternións como matrices de tal xeito que a suma e a multiplicación de cuaternións correspondan á suma e á multiplicación da matriz. Unha delas é usar matrices complexas 2 × 2, e outra é usar matrices reais de 4 × 4. En cada caso, a representación dada é unha dunha familia de representacións linearmente relacionadas. Estas son homomorfismos inxectivos de nos aneis de matrices M(2,C) e M(4,R), respectivamente.
O cuaternión a + bi + cj + dk pódese representar usando unha matriz complexa 2 × 2 como
Usando matrices reais 4 × 4, ese mesmo cuaternión pódese escribir como
Porén, a representación dos cuaternións en M(4,R) non é única. Por exemplo, o mesmo cuaternión tamén se pode representar como
Teorema dos catro cadrados de Lagrange
editar- Artigo principal: Teorema dos catro cadrados de Lagrange.
Os cuaternións tamén se usan nunha das demostracións do teorema dos catro cadrados de Lagrange na teoría de números, que afirma que todo número enteiro non negativo é a suma de catro cadrados enteiros. Alén de ser un teorema elegante por dereito propio, o teorema dos catro cadrados de Lagrange ten aplicacións útiles en áreas das matemáticas fóra da teoría de números, como a teoría do deseño combinatorio. A proba baseada en cuaternións usa cuaternións de Hurwitz, un subanel do anel de todos os cuaternións para os que hai un análogo do algoritmo euclidiano.
Raíces cadradas de −1
editarNos números complexos, hai exactamente dous números, i e −i, que dan −1 ao cadrado. En hai infinitas raíces cadradas de menos un: a solución do cuaternión para a raíz cadrada de −1 é a esfera da unidade en Para ver isto, sexa q = a + b i + c j + d k un cuaternión, e supoña que o seu cadrado é −1. En termos de a, b, c e d, isto significa que
Para satisfacer as tres últimas ecuacións, a = 0 ou b, c e { {mvar|d}} son todos 0. O último é imposíbel porque a é un número real e a primeira ecuación implicaría que a2 = −1. Polo tanto, a = 0 e b2 + c2 + d2 = 1. Noutras palabras: un cuaternión elévase ao cadrado a −1 se e só se é un cuaternión vectorial coa norma 1. Por definición, o conxunto de todos eses vectores forma a esfera unitaria.
Só os cuaternións reais negativos teñen infinitas raíces cadradas. Todos os demais teñen só dúas (ou unha no caso de 0).[b]
Grupos de rotación tridimensionais e de catro dimensións
editar- Artigos principais: Cuaternións e rotación espacial e Operador de rotación (espazo vectorial).
A palabra "conxugación", a maiores do significado dado anteriormente, tamén pode significar levar un elemento a a rar −1 onde r é algún cuaternión distinto de cero. Todos os elementos que se conxugan cun elemento dado (neste sentido da palabra conxugado) teñen a mesma parte real e a mesma norma da parte vectorial. (Así o conxugado noutro sentido é un dos conxugados neste sentido.) [14]
Así, o grupo multiplicativo de cuaternións distintos de cero actúa por conxugación sobre a copia de formada por cuaternións con parte real igual a cero. A conxugación por un cuaternión unitario (un cuaternión de valor absoluto 1) con parte real cos(φ) é unha rotación dun ángulo 2φ, sendo o eixo da rotación a dirección da parte vectorial. As vantaxes dos cuaternións son:[15]
- Evitando o bloqueo do cardán, un problema con sistemas como os ángulos de Euler.
- Máis rápido e máis compacto que as matrices.
- Representación non singular (comparada cos ángulos de Euler, por exemplo).
- Os pares de cuaternións unitarios representan unha rotación no espazo 4D.
O conxunto de todos os cuaternións unitarios (versores) forma unha esfera de S3 e un grupo (un grupo de Lie) baixo multiplicación, como cubrimento do grupo de matrices ortogonais 3×3 reais de determinante 1 xa que "dous" cuaternións unitarios corresponden a cada rotación baixo a correspondencia anterior. Ver truco do cinto de Dirac.
Álxebras de cuaternións
editar- Artigo principal: Álxebra de cuaternións.
Os cuaternións pódense xeneralizar en outras álxebras chamadas álxebras de cuaternións. Considere F calquera corpo con característica diferente de 2, e a e b son elementos de F; unha álxebra asociativa unitaria de catro dimensións pódese definir sobre F con base 1, i, j, e i j, onde i2 = a, j2 = b e i j = −j i (así temos (i j)2 = −a b).
As álxebras de cuaternións son isomorfas á álxebra de matrices 2×2 sobre F ou forman álxebras de división sobre F, dependendo da escolla de a e b.
Notas
editar- ↑ "On Quaternions; or on a new System of Imaginaries in Algebra". Letter to John T. Graves. 17 October 1843.
- ↑ Rozenfelʹd, Boris Abramovich (1988). The history of non-euclidean geometry: Evolution of the concept of a geometric space. Springer. p. 385. ISBN 9780387964584.
- ↑ Hamilton. Hodges and Smith. 1853. p. 60.
quaternion quotient lines tridimensional space time
- ↑ Hardy 1881. Ginn, Heath, & co. 1881. p. 32. ISBN 9781429701860.
- ↑ Mamone, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). "Orientational Sampling Schemes Based on Four Dimensional Polytopes". Symmetry 2 (3): 1423–1449. Bibcode:2010Symm....2.1423M. doi:10.3390/sym2031423.
- ↑ Kunze, Karsten; Schaeben, Helmut (November 2004). "The Bingham distribution of quaternions and its spherical radon transform in texture analysis". Mathematical Geology 36 (8): 917–943. Bibcode:2004MatGe..36..917K. doi:10.1023/B:MATG.0000048799.56445.59.
- ↑ 7,0 7,1 See Hazewinkel, Gubareni & Kirichenko 2004, p. 12
- ↑ Altmann, S.L. Rotacións, cuaternións e grupos dobres. Ch. 12.
- ↑ Gibbs, J. Willard; Wilson, Edwin Bidwell (1901). Vector Analysis. Yale University Press. p. 428.
right tensor dyadic
- ↑ Hamilton, W.R. (1844–1850). "On quaternions or a new system of imaginaries in algebra". David R. Wilkins collection. Philosophical Magazine (Trinity College Dublin).
- ↑ Hamilton, W.R. (1899). Elementos dos cuaternións (2ª ed.). Cambridge University Press. p. 244. ISBN 1-108-00171-8.
- ↑ Perlis, Sam (1971). "Cápsula 77: Cuaternións". Temas históricos en álxebra. Temas históricos para a aula de matemáticas 31. Reston, VA: National Council of Teachers of Mathematics. p. 39. ISBN 9780873530583. OCLC 195566.
- ↑ Porteous, Ian R. (1995). "Capítulo 8: Cuaternions". En Cambridge University Press. Clifford Algebras and the Classical Groups (PDF). Cambridge Studies in Advanced Mathematics 50. Cambridge. p. 60. ISBN 9780521551779. MR 136909>. OCLC 32348823. doi:10.1017/CBO9780511470912.009.
- ↑ Hanson, Jason (2011). "Rotacións en tres, catro e cinco dimensións". arXiv:1103.5263 [math.MG].
- ↑ Günaşti, Gökmen (2016). Quaternions Alxebra, Their Applications in Rotations and Beyond Quaternions (BS). Linnaeus University.
- ↑ A parte vectorial dun cuaternión é un vector "axial" ou "pseudovector", non un vector ordinario ou "polar", como foi formalmente probado por Altmann (1986).[8] Pódese representar un vector polar nos cálculos (por exemplo, para a rotación por un cuaternión "transformada de semellanza") por un puro cuaternión imaxinario, sen perda de información, mais non se deben confundir os dous. O eixo dun cuaternión de rotación "binario" (180°) corresponde á dirección do vector polar representado neste caso.
- ↑ A identificación das raíces cadradas de menos un en foi dada por Hamilton[11] pero omitiuse con frecuencia noutros textos. En 1971, Sam Perlis incluíu a esfera na súa exposición de tres páxinas incluída en Temas históricos en álxebra publicado polo National Council of Teachers of Mathematics.[12] Máis recentemente, a esfera de raíces cadradas de menos un descríbese no libro de Ian R. Porteous Clifford Algebras and the Classical Groups (Cambridge, 1995) na proposición 8.13.[13]4
Véxase tamén
editar| Wikimedia Commons ten máis contidos multimedia na categoría: Cuaternión |
Bibliografía
editar- William Rowan Hamilton (1847). "On quaternions" (PDF).
- "Os quaterniões e suas aplicações" (PDF). Universidade lusíada.
Outros artigos
editar- Conversión entre cuaternións e ángulos de Euler
- Cuaternión dual
- Álxebra exterior
- Ciaternión hiperbólico
- Esfera de Lénárt
- Matrices de Pauli
- Variedade cuaterniónica
- Matriz cuaterniónica
- Polítopo cuaterniónico
- Rotacións no espazo euclidiano 4-dimensional
- Slerp
Ligazóns externas
editar- Paulson, Lawrence C. Quaternions (Formal proof development in Isabelle/HOL, Archive of Formal Proofs)
- Quaternions – Visualisation






