Argumento (análise complexa)

Nas matemáticas, o argumento, abreviado como arg, dun número complexo z é o ángulo entre o eixo real positivo no plano complexo e a recta que une z coa orixe deste plano.

Un número complexo pode ser visualmente representado como um punto localizado no plano complexo. O valor do ángulo $\varphi$ é o argumento do número complexo $z=~x~+~iy$.

Definición

O argumento defínese de dúas formas equivalentes:

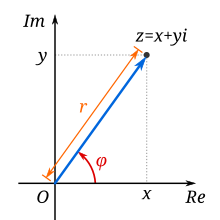
• Xeométricamente, na relación do plano complexo, arg z é o ángulo φ no eixo real positivo representado polo vector z. O valor numérico vén dado polo ángulo en radiáns e é positivo se se mide no sentido antihorario.
• Alxebricamente, un argumento dun número complexo z = x + iy é calquera valor real $\phi$ tal que

$z=x+iy=r\cos \phi +ir\sin \phi \$

para algún r real positivo. A unidade r é o módulo de z, escrito como

$r=|z|={\sqrt {x^{2}+y^{2}}}\ .$

Os termos amplitude ou fase úsanse ás veces para representar esta igualdade.

Baixo ambas as definicións, pódese ver que o argumento para calquera número complexo distinto de cero ten moitos valores posíbeis: en primeiro lugar, como ángulo xeométrico, é evidente que todas as rotacións da circunferencia non alteran o punto, polo que os ángulos diferentes por un múltiplo enteiro de 2π radiáns (nunha circunferencia completa) é o mesmo. Así mesmo, a partir da periodicidade do seno e do coseno, a segunda definición tamén ten esta propiedade.

Notación

A notación para o argumento non é universal. Porén, é común denotalo como $\operatorname {arg} (z)$.

Formularios de cálculo

O argumento a partir dun número complexo $z\,\!$ pódese obter de varias maneiras, incluíndo:

• Dado $z=a+bi\,\!$ (forma rectangular), podemos obter $\operatorname {arg} (z)=\arctan \left({\frac {b}{a}}\right)$;
• dado $z=r(\cos \theta +i\sin \theta )=re^{i\theta }\,\!$ (forma polar e forma exponencial), temos $\operatorname {arg} (z)=\theta$.
• dado $z=a+bi\!$ e sabendo que ${cos\theta }={\frac {a}{|z|}}$ e ${sen\theta }={\frac {b}{|z|}}$, onde $|z|\!$ é a distancia entre $O\!$ e o punto $Z\!$ ; procuramos os valores de sen e cos e así atoparemos na táboa trigonométrica que ángulo ten estes valores para seno e coseno.

Véxase tamén

Outros artigos

• Número complexo.

Ligazóns externas

• argumento-de-um-numero-complexo.